AP微积分有哪些考试套路？（内附复习笔记）

本期分享AP微积分BC干货笔记：

在AP微积分BC的学习中，最后一章压轴出场了一段复杂繁琐的Series判别法则，很多同学做题目时不知道该使用哪种方法，想到了A，结果用成了B，还有同学甚至根本不记得ABC有什么，这些方法被用在判别级数敛散性上（Test Methods for Convergence and Divergence），一个级数的敛散性用正确的方法识别，就好比千里马要遇到属于它的伯乐，怀才不遇的时候最渴望被人赏识认可了吧～

本期干货笔记的主人公：

Test Methods for Convergence and Divergence

本文目录

1.方法分类

2.例题解析

方法分类

1️⃣方法一：The nth Term Test(尾项判别法)

第一种方法也是用起来最简单的方法，我们假定存在级数a_n

如果 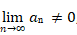，那么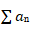diverges(发散)。但是如果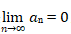，那么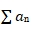是不是就converge（收敛）了呢，此处强调，并不是！此处极限值如果为0，就证明第一种nth Term Test无效，你需要尝试别的方法。

2️⃣方法二：Integral Test (积分判别法)

当正项级数a_n存在时（a_n＞0），设f(n)= a_n , 当正函数f(x)为连续递减函数时（f(x)is positive, continuous and decreasing）,简称当函数f(x)PCD时，广义积分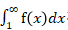存在确定数值，正项级数a_nconverges（收敛）。

3️⃣方法三：Harmonic Series and p-Series（调和级数和P级数）

p级数指的是像此类格式的级数：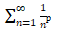

当P＞1,此级数converge（收敛）。

当P≤1，此级数diverge（发散）。

当P= 1，此级数为Harmonic Series（调和级数），由上可知，Harmonic Series（调和级数）发散

✨记忆Shortcut

把P值想象在一根数轴上，以1为临界点，如下图所示，记忆顺序为DHC（Divergent,Harmonic, Convergent）

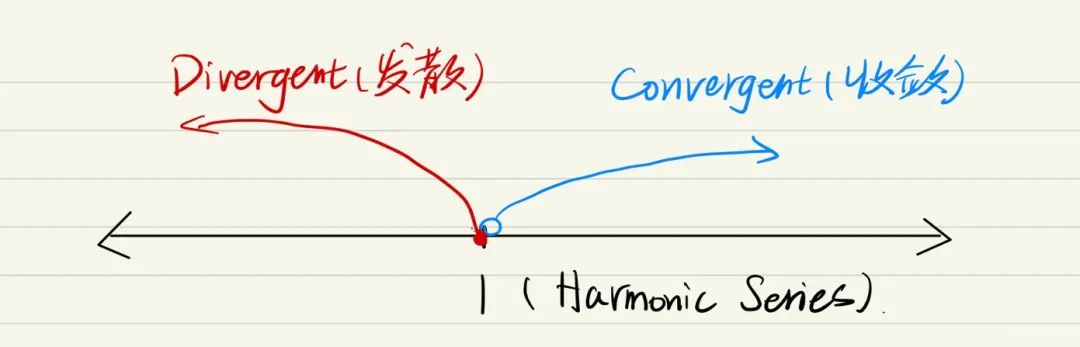
4️⃣方法四：Comparison Test(比较判别法)

设两个正项级数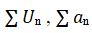，(均大于0)

1. If 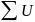_n converges, a_n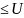n, then 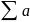_n converges.

2. If 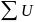_n diverges, a_n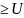n, then 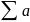_n diverges.

对于P Series特别有用，经常会用到：

✨记忆Shortcut

我们把Convergent（收敛）比作人性格中的“低调”，Divergent（发散）比作“高调”。

由1中可以看到，人物U低调，人物A比U还要低调，那么人物A必然低调。

由2中可以看到，人物U高调，人物A比U还要高调，那么人物A必然高调。

5️⃣方法五：Alternating Series Test (交错级数判别法)

什么是交错级数，顾名思义就是前项后项改变符号，不断交替。

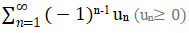
若一个Alternating Series（交错级数，简称AS）收敛，需满足如下两个条件：

1. a_n+1＜a_n, for all n

2. 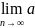_n = 0

这两个条件的准则也被称为Leibniz’s Test（莱布尼茨判别法）。

6️⃣方法六：Ratio Test(比值判别法)

设正项级数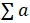，使得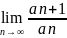= L, 若L< 1, 则级数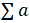converges(收敛)，若L > 1, 则级数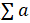diverges（发散）。

7️⃣方法七：Geometric Series (几何级数)

设存在几何级数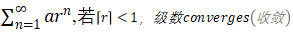

设存在几何级数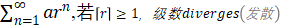

?注：方法六七Convergeor Diverge数值相似，注意与方法三区分。

8️⃣方法八：The limit Comparison Test （极限比较判别法）

此方法与The Comparison Test类似,也称比较判别法的极限形式。

设两个正项级数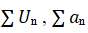，(均大于0)

1. If 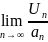= L, 0 < L < 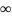, then both 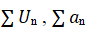converge or diverge.

2. If 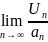= 0, and 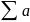_n converges, then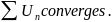

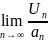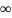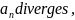3. If = , and then 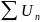diverges.

当使用普通的Comparison Test时，发现找对比级数时有点困难，可以尝试使用The limit Comparison Test。

是不是觉得方法太多还是不太容易记住，那就看这个思维导图吧。

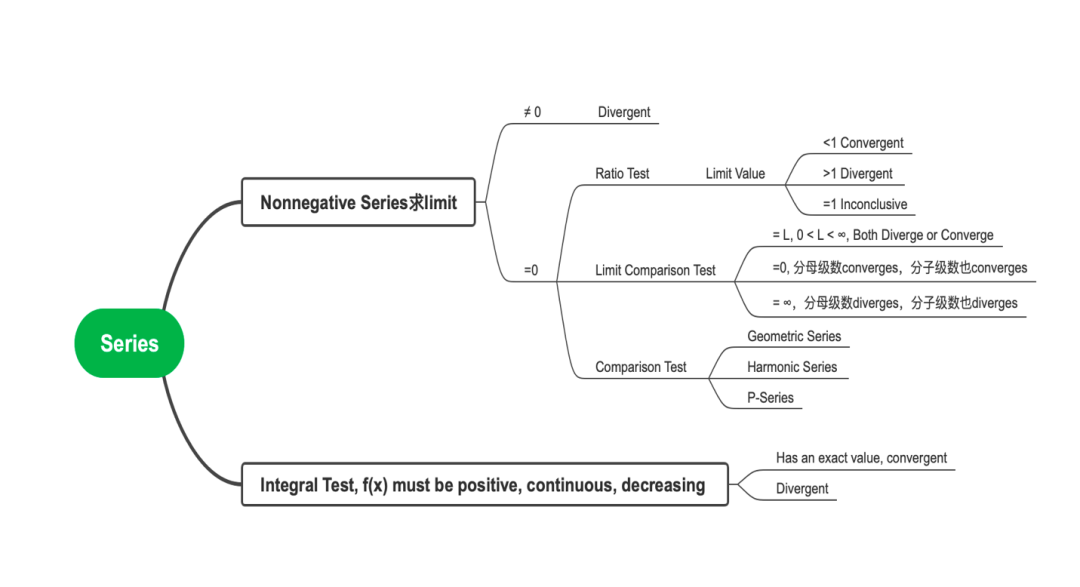
?BonusPart: Absolute Convergence and Conditional Convergence (绝对收敛和条件收敛)

Convergence(收敛)分为绝对和条件，好像有一点点麻烦呢，其实概念定理非常容易理解，对于任意项级数，如果其绝对值级数converge（收敛），那么此级数必然converge（收敛），称为Absolute Convergence(绝对收敛)。

但如果其绝对值级数diverge（发散），但是原级数收敛，则原级数称为Conditional Convergence (条件收敛)。

综上所述，上述文字我们也可以用数学语言来表达：

For 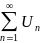,if 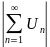converges, so 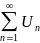is Absolute Convergence.

For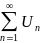,if 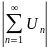diverges, but 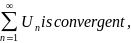so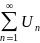is Conditional Convergence.

例题解析

Problem1

Use the nth Term Test

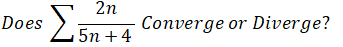
?Solution: 根据nth Term Test定义，当此级数的n值趋于正无穷且极限值不为零时，级数发散。所以我们需要求此级数当n趋于正无穷时的极限值。

From the definition, 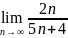=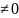,so this series is divergent by the nth Term Test.

Problem2

Use the Comparison Test

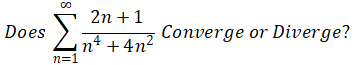
?SolutionA: 这种类型的题目可能乍一看看不出来，那就需要逐步破解，一般分母处次数较高时，我们优先考虑使用Comparison Test。

如题，分母处最高次数为4，所以我们对比级数可以设为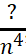,至此，观察上方分子处，还有一次的n，所以整个分数的次数可假设为3，可以假设级数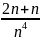与题目级数进行比对。

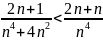
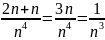
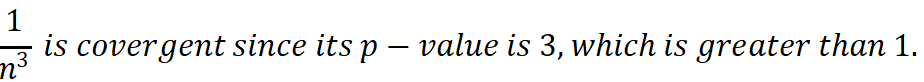
?注:Harmonic Series and P-series可以用数轴记忆法，p>1时，级数converge。

由上方的记忆shortcut知道，比“低调”的级数更低调的级数，必然也“低调”，所以本题。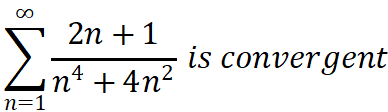

?SolutionB: 使用普通的Comparison Test可能不易比较，此时我们可以尝试使用The limit comparison Test （此方法通常适用于当Comparison Test难以找到比对series时）

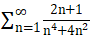观察级数分子分母，分子最高次为1，分母最高次为4，整项次数便可为3，所以原series可以同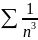进行比较。

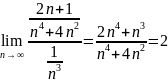
根据limit comparison test定理，limit值大于0时，两个级数拥有同样的敛散性，并且已知p-series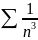 converge（收敛）（p>1）。

Since the limit value is 2, so both series diverge or converge.

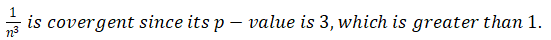
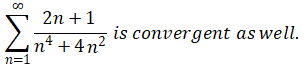
Problem3

Use the Ratio Test

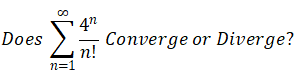
一般对于有factorial（阶乘）的题目，通常使用Ratio Test

所以.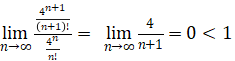

Therefore,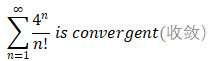

Problem4

Use the Integral Test

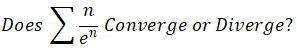
确保series可以使用integral test，要确定这个series是PCD(Positive, Continuous, Decreasing)

?Solution:

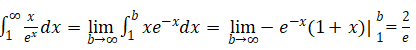
By using the L’Hospital’s Rule, the integral has an exact value, so the series is convergent.

(在求反导的过程中使用integration by parts)

Problem5

Use the Alternating Series Test

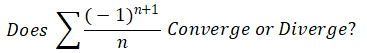
?Solution：当AP考试中出现(-1)ⁿ类似形式的Series时，我们优先考虑使用AST(Alternating Series Test), 其次使用Ratio Test。

若使用AST证明Series Converges（级数收敛），需满足以下两个条件：

1. a_n+1＜a_n, for all n

2. 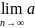_n = 0

Since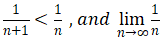=0,原来的级数converge得证。

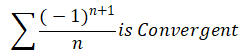
Problem6

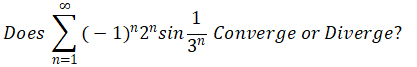
If it is convergent, determine it is absolute convergent or conditional divergent.

?Solution：这个级数融合了Alternating Series（交错级数）和sin函数，看起来较复杂，为了判断此级数为Absolute Convergence or Conditional Convergence,首先确定其绝对值的敛散性，故级数

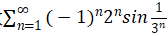的绝对值为2ⁿsin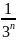,观察绝对值之后的series存在sin函数，由此我们联想到sin函数图像最大值为1，所以可以得到2ⁿsin=

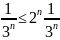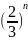
由Geometric Series（几何级数）定理可知，当r<1时，级数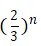

converge（收敛）

至此，由comparison test可知，当一个series比此series更“低调”时，那个series必然“低调”，所以。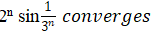

因为此级数是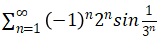

的绝对值，根据定理可知，当级数的绝对值converge(收敛)时，原级数是Absolute Convergence.

Bonus Question

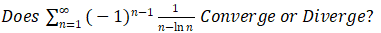
If it is convergent,determine it is absolute convergence or conditional convergence.

?Solution：是不是有那么一点点傻眼（学神忽略），不要紧的，跟着解题步骤一步一步往后推，对于判断Absolute Convergence（绝对收敛），还是Conditional Convergence （条件收敛）的题目，首先取题目中series的绝对值。

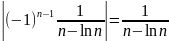
那么级数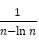是converge还是diverge呢，我们可以使用comparison test，注意到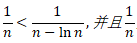是Harmonic  series,which is divergent.

由记忆shortcut可知，比“高调”的更高调的，必然“高调”。所以级数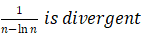（发散）。

至此，我们需要判定Alternating Series 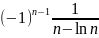是convergent还是divergent，便想到使用AST（Alternating Series Test），记得条件：

1. a_n+1＜a_n, for all n

2. 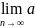_n = 0

看到这里问题又来了，级数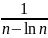是分数，如何比较“a_n+1＜a_n”的大小呢，此处需要动一动聪明的小脑袋，a_n+1＜a_n不可，何尝不试试证明,所以[(n+1)- (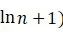]- (n - 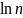)= 1 - 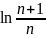> 0 (ln函数最大值小于1)，所以证得,所以a_n+1＜a_n，且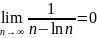，所以根据AST，级数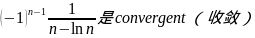，又因为此级数的绝对值Diverge（发散），所以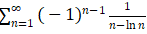是Conditional Convergenct（条件收敛）。

最后的总结

本期的AP Calculus BC干货笔记总结了最后一章节中最难缠的敛散性判别法，我们对考点中的每种方法进行了总结陈述并配上shortcut，在例题部分深入分析，同学们只要牢记习思维导图和部分方法的记忆Shortcut，在AP微积分BC考试中，碰到Series敛散判别的题目一定可以手到擒来。

在复习Unit10 Test Methods for Convergence and Divergence时，注意分清每种方法不要混淆，AP5分不是梦～