微积分在SAT数学中的妙用！

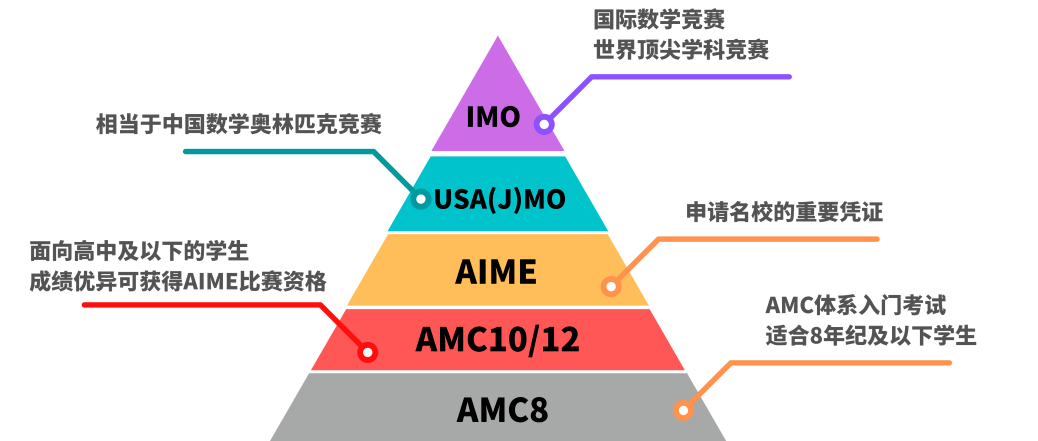
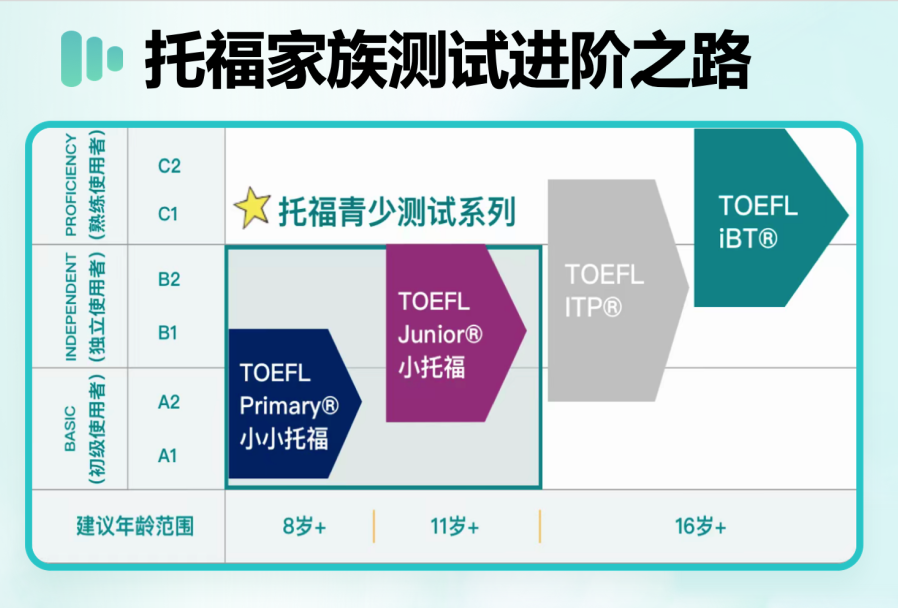
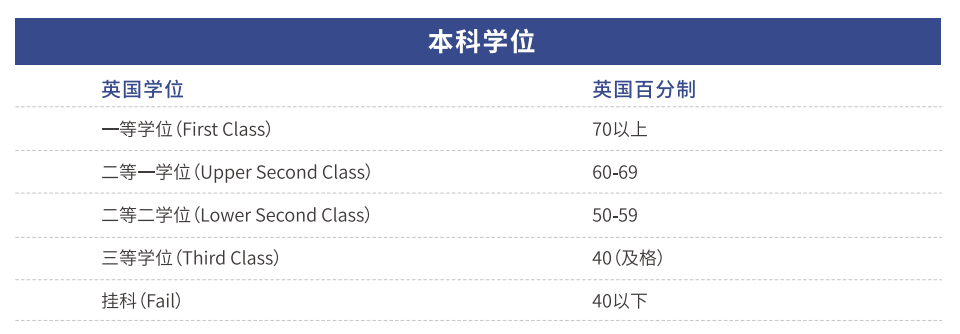
微积分是数学领域中非常常见的工具，也是一门大多学生学习过程中会涉及到的一部分知识点，在人们的学习生活当中都有这个概念的影子。

今天，我们就来聊一聊微积分在SAT数学当中的运用。当然，微积分并不属于SAT数学的考察范围，所以我们只是从工具使用的角度在恰当的地方使用微积分的基础知识。

本文作者：

Part 1

首先，微积分中导数的概念是建立在极限的基础之上的，直观来讲就是一个函数在某一个点上的导数反应了这个点的变化率（rate of change）。

譬如我们知道速度等于路程除以时间

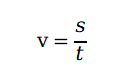
在某段时间里面路程的变成的量除以时长就是这段时间里路程的平均变化率（也就是速度），那如果但这一小段时间无限短的时候它就变成了一个时间点，用一样的方法便能得到在这一个时间点上的瞬时路程变化率（瞬时速度）。

基于前人的研究我们有了直接得到一个函数到函数的各种各样的公式，也就是说我们可以通过这个公式直接快速地得到某个函数上某个点的平均变化率，而其中最为常见的公式便是

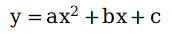
也就是说我们可以直接利用y'这个去分析计算函数上任何一个点的变化率（也就是该点切线的斜率）

Part 2

那么我们如何在SAT数学中利用好它呢？

我们都知道二次函数的standard form是

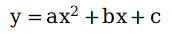
那么它的导函数则应该是

而我们都知道二次函数的图像是parabola，它有一个vertex，而vertex点处的rate of change很明显为0，所以我们就可以得到该点的横坐标应该为y'为0的时候，则

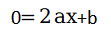
故定点坐标的横坐标为x=-b/2a

大家有没有发现，这里我们用一个非常简单的办法就得到了顶点坐标的公式。

Part 3

在SAT题目中

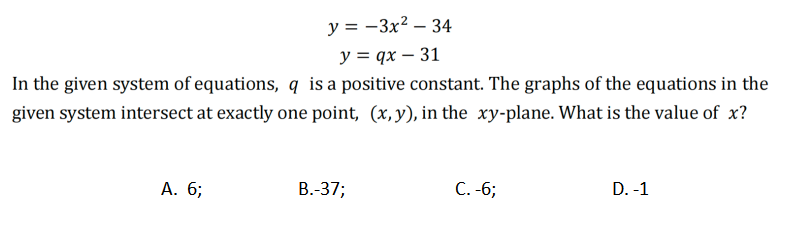
比如这道题目中，因为一个parabola和一条直线相交于一点，也就意味着这条直线便是这个抛物线的切线，所以有

又因为它们只有一个交点，所以可通过判别式discriminant为0直接得到q的值，进而就可得到正确的答案了！

以上就是今天的分享！