2025 UKJMO第五第六题零分惹争议!
前言
2025年UKJMO(Junior Mathematical Olympiad)于6月11日举行,吸引了众多热爱数学的初中生参与。比赛结束后,第五题和第六题的“零分争议”引发了广泛讨论——不少学生提交了清晰过程、画了图,却仍未获得分数。
在新西兰参考学生中,A同学与B同学分别对这两道题提交了解答,学生和家长普遍认为至少应获得“部分分”,但主办方UKMT最终维持原判。
01、第五题争议
构造题不是“举个例子”
而是“穷尽所有可能”
原题如下
For which 𝑛 ≥ 3 can an 𝑛-sided polygon be made by joining several one-by-one squares together edge-to-edge?

这是一道典型的构造类证明题,要求考生说明哪些边数的多边形可以通过正方形拼接形成,并证明其他情况不成立。
01
A同学在解答中提出了一种递归构造方式:从一个正方形出发,每次沿边添加一个正方形,边数随之增加 2,最终形成边数为偶数的多边形。这一构造方法思路清晰,可无限延展,理论上适用于所有偶数 𝑛≥4。
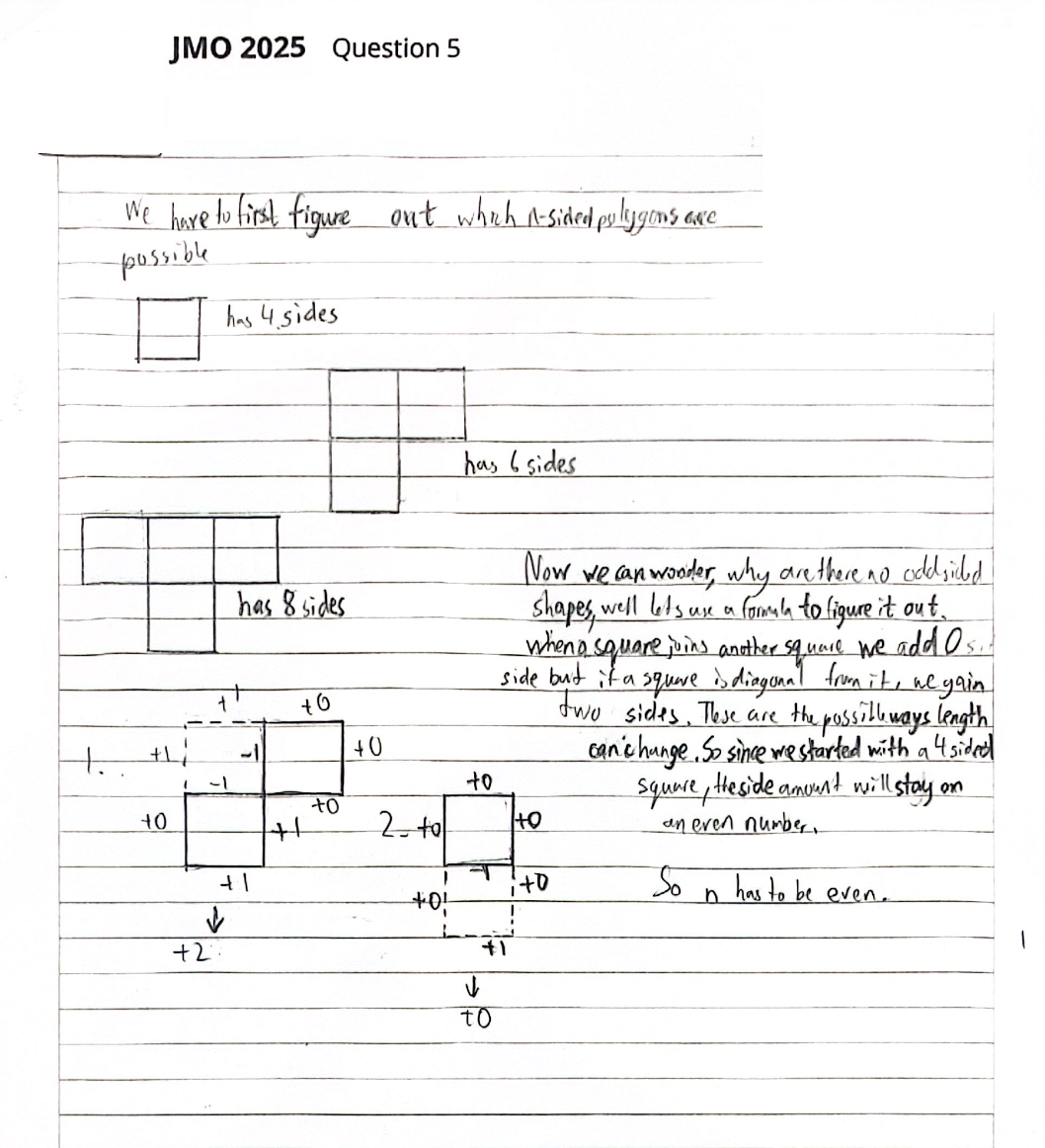
02
然而,UKMT在评卷反馈中指出:
“该解答与多数考生相似,仅构造出一种情况,并未覆盖所有结构情形,因此不给予得分。”

在官方报告中,还特别提到,几乎没有学生考虑所有情况。“每添加一个正方形”这一策略虽然直观,但未能穷尽所有起始结构和边数变化方式,也未严格排除所有奇数边情况。因此,即便思路清晰,也因论证不完整被视为“未完成证明”。
02、第六题争议
猜得对 ≠ “数学证明”
原题如下
The sum of the factors of 2025 is odd. What is the smallest number 𝑁 > 2025 for which the sum of the factors of 𝑁 is odd?

01
B同学注意到完全平方数可能拥有奇数个因子,从而猜测其因子和也可能为奇数。他分析了 2025 = 45² 与 2116 = 46²,使用素因数分解和公式计算因子和为奇数,最终给出答案 2116。

从逻辑链条看,该解答隐含了“完全平方数 → 因子个数为奇 → 因子和可能为奇”这一推演思路,同时借助正确的工具(如因子和公式)进行尝试验证。
02
但 UKMT 在评卷回应中明确指出:
“该解答未对‘完全平方数因子和为奇’这一关键命题给出数学证明,这一结论不是公理,未经证明不能使用,因此不给分”

换言之,尽管B同学展现了正确的观察力、合理的猜想路径和部分计算能力,但由于核心逻辑未加以严谨论证、也未排除 2025 与 2116 之间其他可能数,仍不符合UKMT奥林匹克级别的对于“完整解答”的严谨性评分要求。
03、家长最该关注的问题
01、不是“会做”就能得分,为什么?
许多家长感到疑惑:“明明写了过程,甚至图也画了,怎么还得了零分?”这正是UKJMO最容易被误解、却最关键的评分逻辑:
✔ 构造题,不是找一个例子,而是找出所有可能或说明无其他可能。✔ 结论题,不是猜对就能得分,而是需要“自下而上”的严格论证。
❌缺乏形式化的排除与分类讨论,哪怕结论对,也不计分;
❌ 仅展示“观察力”与“方向感”不够,必须“写出来”一整套推理链。
02、对学生长期发展的启发
1. UKJMO并不鼓励“尝试式”答题,而是鼓励“论证式”思维;
2. 评分标准不容“补脑”加分,即使方向对了、结论猜对了,也必须写出完整论证才得分;
3. 这不是否定孩子的努力,而是对“顶尖思维表达”的训练要求。
这是否严苛?或许从常规考试角度来看是。但正因如此,它才具有高含金量,才是真正筛选“能解决问题且能清晰表达推理过程”的人才。
03、更应该关注的是
所以我们更应该关注的,不是“这次没拿分”,而是如何在日常训练中,让学生习惯:
•“写出来”的逻辑链条而非“脑中完成”的推理;
• 用“分类讨论”“穷尽情况”“反证法”等完整的工具表达思想;
• 对“显而易见”的猜测保持怀疑,要求形式化推理支撑;
• 理解数学不是“发现现象”,而是“解释现象”。
这些,才是数学教育最深远的价值所在。
04、从比赛中看出真实差距
01、不是没天赋,而是训练不到位
在我们支持下参赛的学生中,普遍具备较强的运算力、逻辑直觉,甚至能发现某些通项模式。但在需要严谨书写完整解法、解释为何没有其他解时,就常常显露出训练的薄弱:
• 缺乏分类讨论与穷尽意识(“为什么其他不行”);
• 语言表达模糊,论证过程不规范
这些不是理解力的问题,而是缺乏奥数写作训练与系统化表达引导。
如果平时只刷题而缺乏奥数写作训练,那么在 UKJMO 这种比赛中,即便思路正确,结果也容易是零分。
02、真正的奥数力,需要肌肉记忆般的训练
UKJMO 不是靠临时冲刺就能应对的,它需要:
•长期积累的逻辑表达能力
•对于讲题方式的语言感和结构感(而不是只给答案)
•对“显然成立”命题背后的怀疑与验证。
只有在专业教师引导下,配合规范的表达训练,才能真正建立“能写出清晰证明”的能力,而这正是未来高阶数学学习的根本。
如何为UKJMO做好准备?
一次比赛的得分,不足以定义一个孩子的数学能力。但一次比赛的评分标准,却能照出孩子是否已具备高层次的思维表达结构。
UKJMO的训练目标,是让学生习惯:
• 把“脑中直觉”写成“外化逻辑”;
• 用完整的论证语言表达复杂想法;
• 把“发现现象”转化为“解释现象”。
如果你的孩子热爱数学、有思考力、有表达意愿,现在就可以开始系统训练。在这条路上,我们愿成为你最专业的支持者。