冲刺P3高分!2024年爱德思夏季大考真题全解析(一)在上半部分,我们已经逐一剖析了2024年爱德思P3夏季大考的前5道题目,相信大家对P3的考查风格和难度有了一定的把握。现在,我们马不停蹄,进入下半场的学习!这部分通常包含了一些分值更高、综合性更强的压轴题型,也更能体现P3的挑战性。希望大家继续保持专注,跟紧我们的节奏,一起攻克第6题到第9题的难关,拿下P3高分!
Q6

 老师点评:这道题是一道非常经典的P3函数综合题,主要考察了复合函数求值、反函数的求解以及解复合函数方程。
老师点评:这道题是一道非常经典的P3函数综合题,主要考察了复合函数求值、反函数的求解以及解复合函数方程。
(a)小问 - 复合函数求值gf(2):对于复合函数求值,比如gf(x),大家一定要记住运算顺序:从内到外。先计算里面的函数f(2) 的值。然后把f(2) 得到的结果,再代入到外面的函数 g(x) 中,计算 g(f(2))。计算时细心一点,这部分通常是送分点。
(b)小问 - 求反函数 f⁻¹(x):求反函数是我们P3必须掌握的核心技能。常规步骤如下:设y = f(x): 把原函数写成 y = ...x... 的形式,例如本题是 y = 6 - 21/(2x + 3)。
反解x: 通过代数变形,把这个式子整理成 x = ...y... 的形式,也就是让 x 成为式子的主语。这一步考验大家的代数基本功。交换x 和 y: 把上一步得到的 x = ...y... 中的 x 和 y 互换位置,得到 y = ...x...。
写出反函数:将新得到的y = ...x... 的 y 替换为 f⁻¹(x),即 f⁻¹(x) = ...x...。一个非常关键的点是反函数的定义域:原函数f(x) 的值域 (Range) 就是其反函数 f⁻¹(x) 的定义域 (Domain)。
所以,在求完反函数的表达式后,一定要记得确定并写出它的定义域。(c) 小问- 解复合函数方程 gg(x) = 126:解这类复合函数方程,思路是:构建复合函数表达式:先写出gg(x) 的具体表达式。gg(x) 就是把 g(x) 的表达式 x² + 5 整体代入 g(x) 中的 x,得到 (x² + 5)² + 5。
建立并解方程:令(x² + 5)² + 5 = 126。这个方程看起来复杂,但其实解起来并不难。整理后得到(x² + 5)² = 121。开平方时注意有正负两种情况:x²+ 5 = 11 或 x² + 5 = -11。对于x² + 5 = 11,得到 x² = 6,解出 x = ±√6。对于x² + 5 = -11,得到 x² = -16,这个在实数范围内无解。
本题的这个复合函数方程,本质上化简下来就是一个关于x² 的一元二次方程,或者说是一个四次方程的特殊形式,没有涉及到特别复杂的三角函数或指对数运算,相对还是比较直接的。总的来说,这道题全面考察了函数的基本操作,只要掌握了复合函数的运算规则、反函数的求解步骤(特别是定义域!),以及解基本代数方程的技巧,拿分还是比较稳的。
Q7


老师点评:这道题是在我们P2学习的stationary point(驻点)知识基础之上,进一步融入了P3关于函数分析与变换的核心考点,综合性比较强。
(a)小问 - 证明导数形式:这部分主要考察大家对复杂函数求导的掌握,特别是乘法法则(Product Rule) 和链式法则 (Chain Rule) 的熟练运用。将 f(x) 看成两部分相乘,分别求导后再用乘法法则组合起来。后续的代数化简,包括通分、合并、提取公因式,也是拿到满分的关键步骤。
(b)小问 - 找出P点 (minimum turning point) 坐标:求驻点,我们知道是令f'(x) = 0。解这个方程可能会得到多个 x 值。这时候,结合题目给出的图像来判断就非常重要了。
从图像上可以清晰地看到函数有两个驻点,而题目要求的P点是一个 minimum turning point(极小值点),并且其 x 坐标为负值。根据这个信息,我们就能从解出的 x 值中选出正确的那一个,再代回原函数 f(x) 计算对应的 y 坐标。
(c)小问- 求 g(x) = -4f(x) 的值域:这问考察的是函数变换对值域的影响。首先,我们要确定原函数f(x) 在其定义域内的值域。结合(b)问找到的最小值点,以及函数在定义域边界和趋向无穷时的行为,可以得到 f(x) 的值域。
然后,再看g(x) = -4f(x) 这个变换。它相当于对 f(x) 的值域先乘以4,再乘以-1。特别注意,当乘以一个负数时,值域的上下界会发生“翻转”,不等号的方向也要改变。
(d)小问 - 点Q在变换下的映射:这一问有一个常见的陷阱需要大家特别注意!题目说点Q(1/2, 3/2) 在曲线 C (即 y=f(x)) 上。
然后曲线 C 经过一系列变换得到新曲线 y' = 40f(x' - 3/2) - 8。问原来的点Q会映射到新曲线上的哪个点。很多同学可能会误以为,新点的横坐标还是1/2,然后去代入新的函数表达式,这是完全错误的!
正确的理解是:点Q的坐标(x_Q, y_Q) 满足 y_Q = f(x_Q)。 一个需要警惕的地方是,题目直接给的 Q(1/2, 3/2),但如果我们自己算 f(1/2),会发现 f(1/2) = 3/8,而不是 3/2。
根据往年经验和Mark Scheme,通常我们应该以函数定义为准,即原始点应为 (1/2, 3/8)。(这里我会按Mark Scheme的思路,用计算出的f(1/2)值)函数图像的变换规则是y -> 40y - 8,x -> x + 3/2 (因为函数内部是 x - 3/2)。
所以,原点(x_old, y_old) 变换后的新点 (x_new, y_new) 满足:x_new = x_old + 3/2y_new = 40 * y_old - 8将我们计算出的Q点实际坐标(1/2, 3/8) 代入上述变换规则,就能得到新点的坐标。
千万不要混淆了:变换的是整个函数图像,原来的点Q也会跟着这个规则移动到新的位置,它的横纵坐标都会发生改变,而不是保持横坐标不变。
总的来说,这道题从求导到驻点分析,再到值域和点变换,考察点比较全面。只要大家基本功扎实,理解函数变换的本质,并注意题目中的细节和潜在“陷阱”,就能顺利解答。
Q8
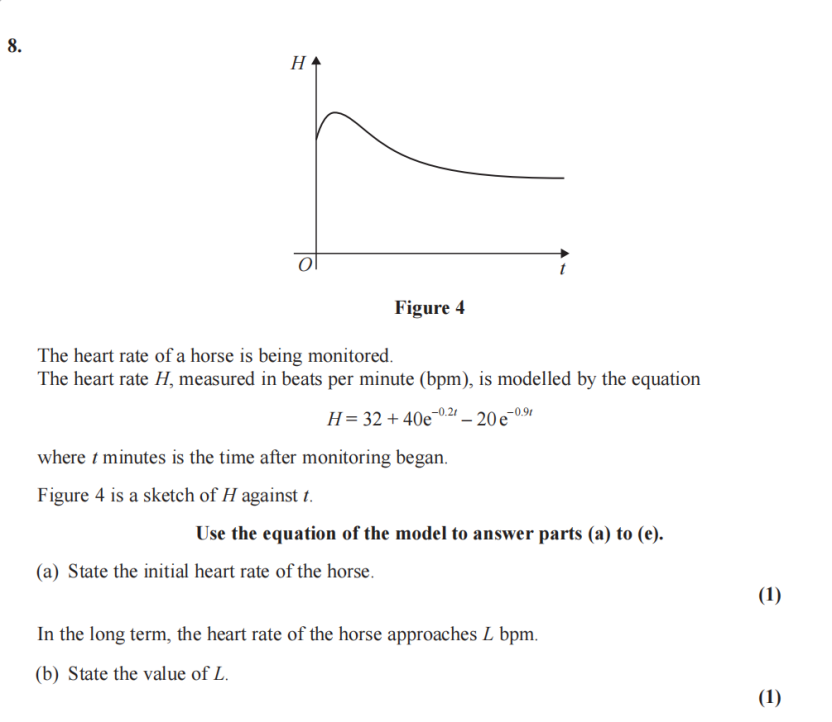


老师点评:这道题是一个非常典型的P3综合大题,它巧妙地将指数模型、微积分(求导找极值)以及数值方法(迭代)结合在了一起,全面考察大家的综合应用能力。题目背景理解:首先,拿到这种应用题,我们要先搞清楚模型描述的是什么。
这里是研究马的心率(H) 随时间 (t) 变化的规律。
(a)小问 - 初始心率 (initial heart rate):当题目中出现关键词“initial”(初始的),它通常意味着自变量为零的时刻。在这个模型里,就是 t = 0 的时候,代表时间刚开始。
我们直接将 t = 0 代入心率公式 H 中计算即可。记住 e^0 = 1,这部分基本是送分点。(b)小问 - 长期心率趋势 (in the long term):与“initial” 相对,“in the long term”(从长远来看)意味着时间 t 趋向于正无穷大 (t → +∞)。
我们需要分析当 t 非常大时,模型中各项的行为。通常,像 e^(-kt) (其中 k > 0) 这样的项,当 t → +∞ 时,e^(-kt) → 0,也就是说这一项会趋近于零。把这个考虑到模型里,就能得到心率的长期稳定值 L。
(c) 小问- 心率最大值点 T:求函数的最大值或最小值点,我们的标准方法是求导数,并令导数等于零,即dH/dt = 0。求导:对心率函数H 关于 t 求导。
这里涉及到指数函数的求导,并且通常伴随着链式法则 (Chain Rule) 的应用。比如 d/dt (e^(at)) = a * e^(at),很多同学容易在求导时漏掉指数上的常数因子 a。
解方程:令dH/dt = 0 后,我们会得到一个关于 t 的指数方程。解这类方程,常用的技巧是两边同时取自然对数 (ln),将其转化为对数方程来解,利用对数的性质(如 ln(e^x) = x, ln(A/B) = lnA - lnB 等)会使求解过程更简单。题目明确说了“不允许完全依赖计算器技术”,所以详细的求导和解方程步骤是必须展示的。
(d)小问 - 证明 M 是某方程的解 (Show that…):这类“Show that” 的问题,本质上是考察我们的代数变形和逻辑推理能力。我们需要从题目给定的条件(当 t = M 时,H = 37)出发,通过一步步严谨的代数运算,将初始的等式逐渐变换成目标方程的形式。关键在于观察目标方程的结构,有目的地进行移项、合并、提取公因式、两边取对数等操作。
(e)小问 - 迭代法求解:这部分是常规的数值方法(迭代法)考查。
计算t₂: 题目会给出迭代公式 t_(n+1) = ...t_n... 和初始值 t₁。我们只需将 t₁ 的值代入迭代公式的右边,计算出 t₂。记得把完整的迭代公式和代入的 t₁ 值写清楚。
求M (迭代收敛值): M 是当迭代次数足够多时,t_n 序列收敛到的那个稳定值。我们需要不断地将前一次迭代得到的结果代入公式,计算出下一个值,直到连续两次迭代的结果在题目要求的精度下不再变化。
一个重要的计算技巧:在迭代的中间过程中,我建议大家尽量多保留几位小数,比如保留七八位有效数字。因为过早地四舍五入会累积误差,影响最终结果的准确性。只在最后一步输出答案时,再根据题目要求的有效数字或小数位数进行四舍五入。
总的来说,这道题分值高,考点多,但只要我们把每个部分涉及的知识点掌握扎实,比如指数函数的性质、求导法则、解指数/对数方程的技巧、代数变形能力以及迭代法的步骤,就能分步攻克,拿到理想的分数。
Q9


老师点评:这道题作为我们这套P3卷子的压轴大题,分值高(14分),考点也相当综合,对大家的各项能力都是一个全面的检验。我们一步步来看:
(a)小问 - 求导 f'(x):这部分相对直接,主要考察的是商法则(Quotient Rule) 的应用。对于 f(x) = u(x) / v(x) 这样的分式函数,其导数 f'(x) = [v(x)u'(x) - u(x)v'(x)] / [v(x)]²。
大家只要牢记商法则的公式,并细心计算 u'(x) 和 v'(x),然后代入并化简,通常问题不大。注意展开和合并同类项时的准确性。
(b)小问 - 求法线方程:这是典型的考察切线与法线关系的题目。核心关系:切线和法线是互相垂直的,所以它们的斜率相乘等于-1 (即 m_切 * m_法 = -1 或 m_法 = -1 / m_切)。
求切线斜率:我们需要利用(a) 问求得的导数 f'(x)。将点P的x坐标代入 f'(x),就能得到曲线在P点处的切线斜率。
求法线斜率:根据上面的核心关系,由切线斜率计算出法线斜率。
求法线方程:我们已经知道了法线的斜率,并且题目告知法线过点P。
利用点斜式方程 y - y₁ = m(x - x₁),就可以很容易地写出法线的方程,并整理成题目要求的形式。
(c) 小问- 函数形式转换 (代数长除法):这问要求将f(x)(一个分子为二次,分母为一次的假分式)改写成 Ax + B + D/(2x + 1) 的形式。核心方法是代数长除法(Algebraic Long Division)。我们将分子 (6x² + 4x - 2) 除以分母 (2x + 1)。
商的部分应该是一个一次多项式(Ax + B)。余数的部分(D) 会作为新的分式的分子,分母不变。通过长除法,我们可以直接得到A、B 和 D 的值。我个人更推荐大家直接用长除法来做这道题。
虽然理论上也可以用系数比较法(即假设f(x) = Ax + B + D/(2x + 1),然后通分,再比较分子各项系数),但对于这个稍微复杂一点的式子,系数比较法在展开和匹配系数时,涉及到较多的项和正负号,更容易出错。
长除法步骤清晰,反而更稳妥。(d)小问 - 定积分求阴影面积:这是压轴题的“重头戏”,考察定积分求面积,并且涉及到组合图形面积的分割与计算。
面积分割策略:观察阴影区域R的形状,它通常不是一个能用单一积分直接求出的简单图形。一个常见的处理方法是,过关键点(比如这里的P点)作垂直于x轴的辅助线,将不规则的区域R分割成几个我们更容易处理的子区域。比如这里,可以分割成曲线 C 下方的一个曲边梯形面积,和法线 l 下方的一个直角三角形面积。
确定积分上下限:对于每个子区域,我们需要准确找到它们在x轴上的积分区间(上下限)。这可能涉及到求解曲线与x轴的交点、直线与x轴的交点,以及题目给定的点P的x坐标。
进行定积分计算:对于曲线C 下方的面积,我们需要对 © 问中得到的 f(x) 的新形式 Ax + B + D/(2x + 1) 进行积分。特别注意,积分 ∫ D/(2x + 1) dx 时,会涉及到链式法则的逆运算,即积分结果是 (D/2)ln|2x+1|,不要漏掉那个 1/2。
对于直线(如法线l)下方的面积,如果它形成的是规则图形(如三角形或梯形),可以直接用几何公式计算面积,这样更简便。如果用积分,也是对直线方程积分。
展示详细过程:题目明确要求“algebraic integration” 和 “exact area”,并且不能完全依赖计算器。
这意味着我们必须详细展示积分的每一步,包括不定积分的求解、代入上下限的过程,以及最终结果的精确形式(如题目要求的 P + Qln3)。不能直接给一个计算器算出来的数值结果。总而言之,这道压轴题虽然综合性强,步骤多,但每一个小问考察的都是我们P3的核心知识点。
只要大家基础扎实,思路清晰,计算仔细,并且能够把不同模块的知识灵活地串联起来,就一定能够成功解答。至此我们已经完成了对2024年爱德思P3夏季大考全部九道题目的精讲。
通过对整套试卷的分析,大家可以看到,P3的题目往往综合性强,计算量和思维量都比较大,但万变不离其宗,核心还是考察大家对基本概念、公式定理的理解和灵活运用能力。
从三角函数到微分积分,从指数对数到数值方法,每一块知识点都需要我们扎实掌握。希望通过这次的真题解析,同学们不仅掌握了具体题目的解法,更能从中总结出P3的常考重点和备考策略。平时一定要多加练习,注重理解,遇到难题不要怕,拆解分析,逐个击破。
想要获取更多P3及其他科目的备考资料、学习技巧和最新考试资讯,请持续关注我们,我们会继续为大家带来更多优质内容!
最后,预祝各位同学在接下来的P3考试中沉着应战,发挥出自己的最佳水平,取得优异成绩!加油!